To learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306Triangles come either in degree angles or 4590 degree angles Also available are triangles with an inking edge for ruling pens We feature Lance triangles as well as steel triangles for professional use and Art Alternative triangles for student use Draw an equilateral triangle all sides are equal and the angles are all 60 deg From any angle drop a line perpendicular to the base(an altitude) By triangle congruence laws you can prove the 2 resulting triangles are congruent which means the al

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
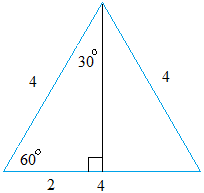
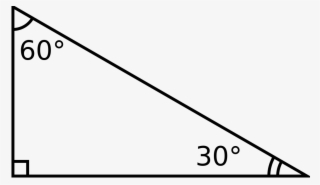
Triangle with 30 60 90 degree angles
Triangle with 30 60 90 degree angles-Constructing a right triangleA triangle is a unique right triangle It is an equilateral triangle divided in two on its center down the middle, along with its altitude A degree triangle has angle measures of 30°, 60°, and 90° A triangle is a particular right triangle because it has length values consistent and in primary ratio
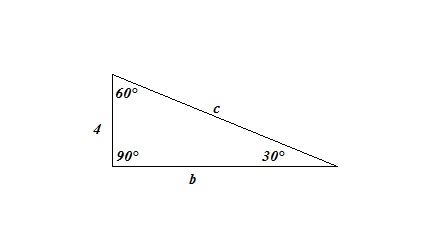



If You Have A Right Triangle 30 60 90 Degree Angles And You Have The Smallest Size Width To Be 4 How Do I Solve For X The Length Of The Triangle Socratic
A right triangle has one angle that is 90 degrees – and this makes these triangles the easiest to cut Take a triangle for example Take a triangle for example If you want the 30 degree angle on the short side of the board, you can make a right triangle with a single cutThe following special angles chart show how to derive the trig ratios of 30°, 45° and 60° from the and special triangles Scroll down the page if you need more examples and explanations on how to derive and use the trig ratios of special angles Trigonometric Function Values Of Special Angles How to derive theSimilar triangles In fact, infinite triangles of this dimension are all similar triangles
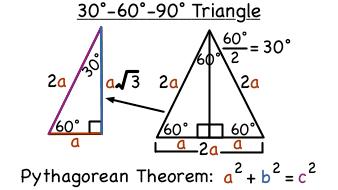
Ludwig Precision 12" Degree Aluminum Drafting Triangle, 012 West Coast Paracord 9 Piece Mathematics Tool Set – Straight Ruler, 30/60/90 Triangle Ruler, 45/90 Triangle Ruler, 180 Degree Protractor and More!Then ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progressionA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room
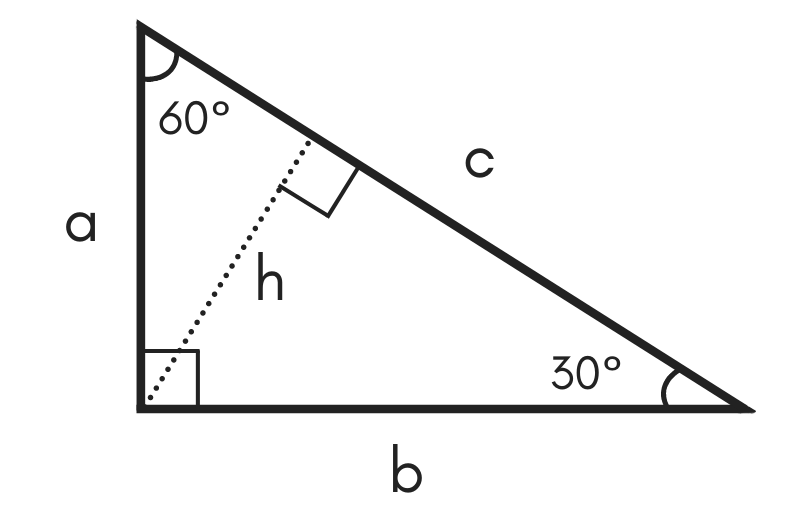
This is a triangle with one side length given Let's find the length of the other two sides, a and b Since the side you are given, 8, is across from the 30 degree angle, it will be the A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another



30 60 90 Triangle Geometry Help




This Printable Triangle Has Angles Of 30 60 And 90 Degrees At Its Vertices Sewing Seam Allowance Hand Stitching Techniques Printable Ruler
A triangle is a right triangle where the three interior angles measure 30° 30 °, 60° 60 °, and 90° 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sidesA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and the longer leg is the square root of 3 timesA draftsman's triangle always has one right angle 90° 30/60/90 triangles draw 90° vertical plus 30° and 60° angled lines 45/90 triangles draw 90° vertical and 45° angled lines Adjustable triangles draw 90° vertical plus various angled lines DraftingSteals large selection of triangles are ideal for the classroom, professional artist



30 60 90 Triangle Definition Theorem Formula Examples




30 45 60 90 Degree Angle Block Ruler Inch Metric Triangle Metal Block Angle Precision Machinist Measurement Tool 2pcs Set Gauges Aliexpress
Triangle30 60 90 This printable triangle has angles of 30, 60, and 90 degrees at its vertices Please make sure to print at 100% or actual size so the rulers will stay true to size My safe download promise Downloads are subject to this site's term of useHow To Construct A 30 Degree Angle A 30 ° angle is half of a 60 ° angle So, to draw a 30 °, construct a 60 ° angle and then bisect it First, follow the steps above to construct your 60 ° angle Bisect the 60 ° angle with your drawing compass, like this Without changing the compass, relocate the needle arm to one of the points on the rays In any triangle, you see the following The shortest leg is across from the 30degree angle The length of the hypotenuse is always two times the length of the shortest leg You can find the long leg by multiplying the short leg by the square root of 3




30 60 90 Triangle Calculator Formula Rules



The Easy Guide To The 30 60 90 Triangle
This printable triangle has angles of 30, 60, and 90 degrees at its vertices Free to download and printCheck out this tutorial to learn about triangles!A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




Test Prep Thursday Special Right Triangles Mathnasium




30 60 90 Triangle Definition Theorem Formula Examples
Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inAnswer (1 of 5) Why in a triangle is the the side opposite 60 degrees x (sqrt(3))?It is based on bisecting an equilateral triangle and using the Pythagorean theorem A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a




How To Use The Special Right Triangle 30 60 90 Studypug



The Easy Guide To The 30 60 90 Triangle
In any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, and you can find the length of the long leg by multiplying the short leg by the square root of 3We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angle Because the interior angles of a triangle always add to 180 degrees, the third angle must beA triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video
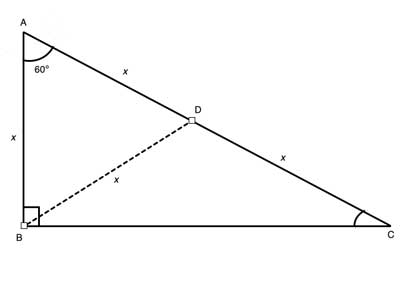
a/c = sin (30°) = 1/2 so c = 2a b/c = sin (60°) = √3/2 so b = c√3/2 = a√3 Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given Example 3 Construct a triangle with measures of 30, 60, and 90 degrees Example 3 Solution Again, since construction doesn't use measurements, we can also think of this as constructing a triangle with a right angle, an angle that is onethird of a straight line, and an angle that is onesixth of a straight lineTriangle ABC shown here is an equilateral triangle Since it's equilateral, each of its 3 angles are 60 degrees respectively Its sides are also equal If we draw a line AD down the middle to bisect angle A into two 30 degree angles, you can now see that the two new triangles inside our original triangle are triangles
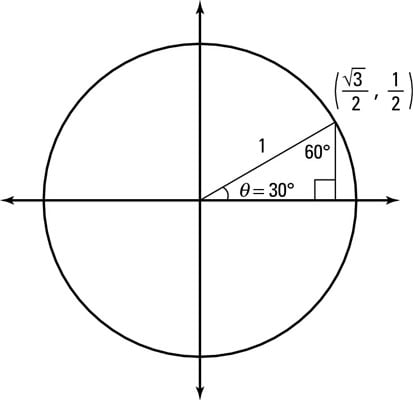



How To Plot The Major Angles Of The Whole Unit Circle Dummies




If You Have A Right Triangle 30 60 90 Degree Angles And You Have The Smallest Size Width To Be 4 How Do I Solve For X The Length Of The Triangle Socratic
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle ) Because the angles are always in that ratio,A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1sqrt (3)2 That is to say, the hypotenuse is twice as long as the shorter leg, andA triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are



Using The 30 60 90 Triangle To Find Sine And Cosine




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
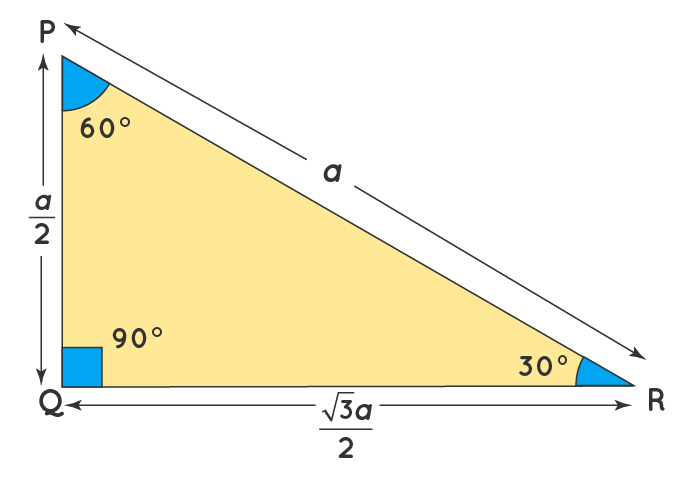
A triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32




Triangle Gma Is 30 Degree 60 Degree 90 Degree If M 26 Cm Find A And S Study Com




30 60 90 Triangle Theorem Ratio Formula Video
The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5(30°60°90°) is a special triangle One of the set squares in the geometry box is of this dimension Normally, the set square has a cut out with in it of same shape but different size;A triâgle of 30 6090 is a special triangle special (a right triangle that is any triangle that contains a 90 degree angle) that always has 30 degree aforemention, 60 degrees and 90 degrees Because it is a special triangle, also has lateral length values that are always in a consistent relationship between each other




Amazon Com Pacific Arc Drafting Triangle 4 Inch 30 60 90 Degrees Topaz Office Products



If A Right Angled Triangle 30 60 90 Hypotenuse Is 10 Cm Then What Is The Length Of The Side Opposite To 60 Angle Quora
Enhance your purchase 12" LENGTH – Aluminum drafting triangles are useful tools for educational and professional use 30° / 60° / 90° DESIGN – Drafting triangle features holes up to 1" in diameter ALUMINUM CONSTRUCTION – Drafting triangles made from highquality aluminum for longterm use without cracking or discolorationClear/Black Includes Sturdy Storage CaseSpecial Right Triangles 30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the



Triangle Ruler Square Set 30 60 45 90 Degrees 27cm Triangle Rafter Angle Ruler 2 Pack Walmart Com
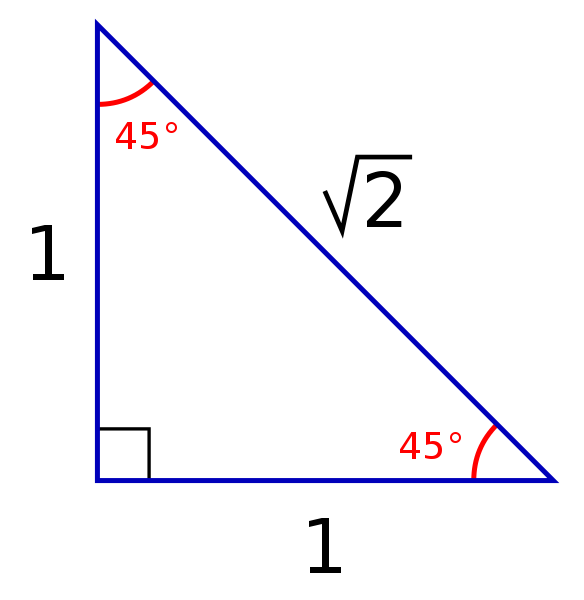



30 60 90 Triangle Formulas Rules And Sides Science Trends
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideThe triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°Get Free 30 60 90 Triangle Answers Algebra 2 A Quick Guide to the Degree Triangle dummies The correct answer is Choice (A) If one of the angles is 30 degrees, the other angle is 60 degrees, making this a triangle, with a side ratio of The 2 is the hypotenuse, making the other Page 14/42




How To Work With 30 60 90 Degree Triangles Education Is Around



A 30 60 90 Triangle Math Central
Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° angles




30 60 90 Triangle Theorem Ratio Formula Video
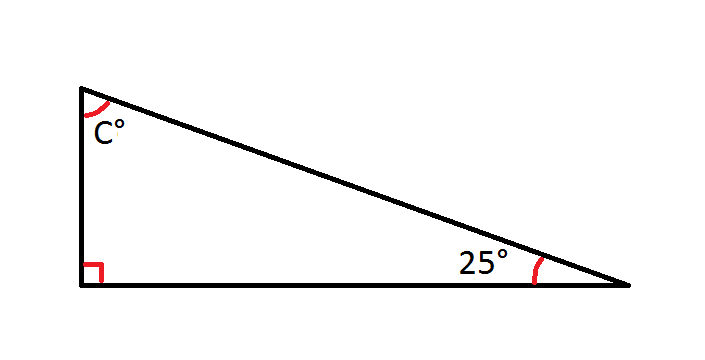



How To Find An Angle In A Right Triangle Basic Geometry
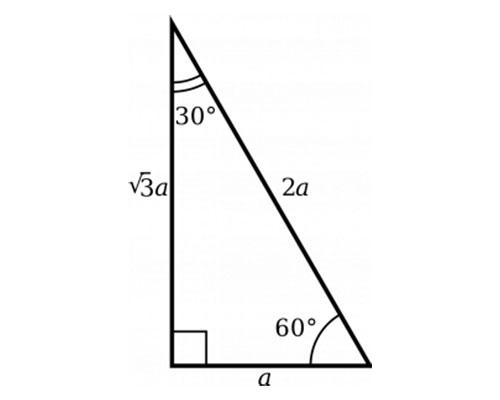



30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
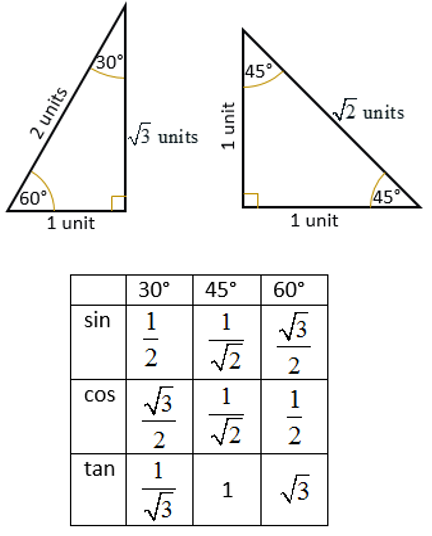



Trigonometric Ratios Of Special Angles 0 30 45 60 90 Video Lessons Examples And Solutions



Precalculus Notes Trig 3




30 60 90 Triangle Theorem Ratio Formula Video
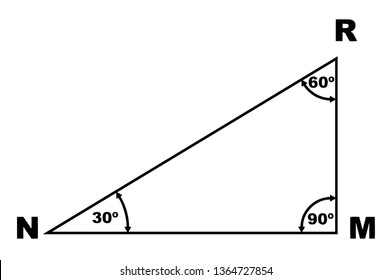



60 Degrees Triangle Images Stock Photos Vectors Shutterstock




30 60 90 Triangle Explanation Examples




A Quick Guide To The 30 60 90 Degree Triangle Dummies




In A 30 60 90 Right Triangle The Side Opposite The 30 Degree Angle Is Brainly Com




Precision Machinist Measurement Tool 2pcs 30 45 60 90 Degree Angle Block Ruler Inch Metric Triangle Metal Block Angle Gauges Aliexpress
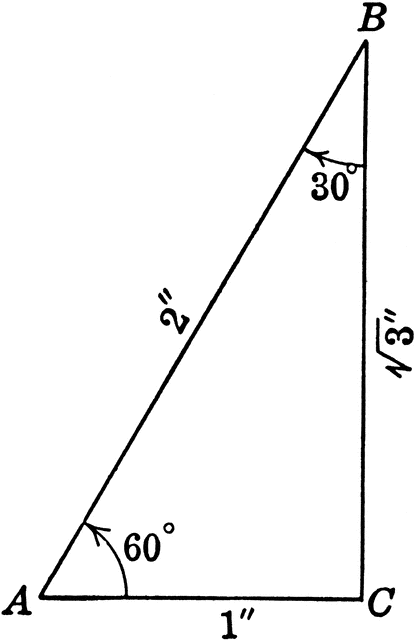



Special Right Triangle With Angles 30 60 90 Degrees Clipart Etc



30 60 90 Triangle 30 Degree Right Angle Transparent Png 1024x592 Free Download On Nicepng



1




Special Right Triangles Flashcards Quizlet




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



30 60 90 Special Right Triangle Calculator Inch Calculator



A 30 60 90 Triangle




Amazon Com Pacific Arc Drafting Triangle 14 Inch 30 60 90 Degrees Fluorescent Orange Office Products




30 60 90 Triangle Explanation Examples



Don T Hate On High School Math Special Right Triangles 30 60 90



Pacific Arc Drafting Triangle 12 Inch 45 90 Degrees Topaz Walmart Com



What Is A 30 60 90 Degree Triangle Virtual Nerd
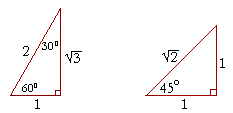



The 30 60 90 Triangle Topics In Trigonometry




Solved Directions Complete The Following Constructions Chegg Com



1




Lesson 11 Triangles 30 60 90 Geogebra




Printable 30 60 90 Degree Triangle Epp Template Instant Pdf Etsy




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle




Solved Directions Complete The Following Constructions Chegg Com




30 60 90 Triangle Explanation Examples
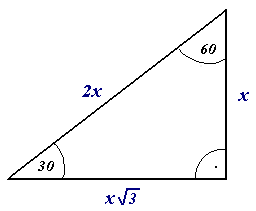



File Triangle 30 60 90 Rotated Png Wikimedia Commons




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules
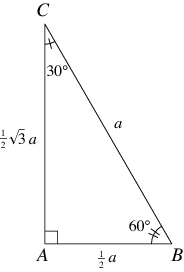



30 60 90 Triangle From Wolfram Mathworld




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
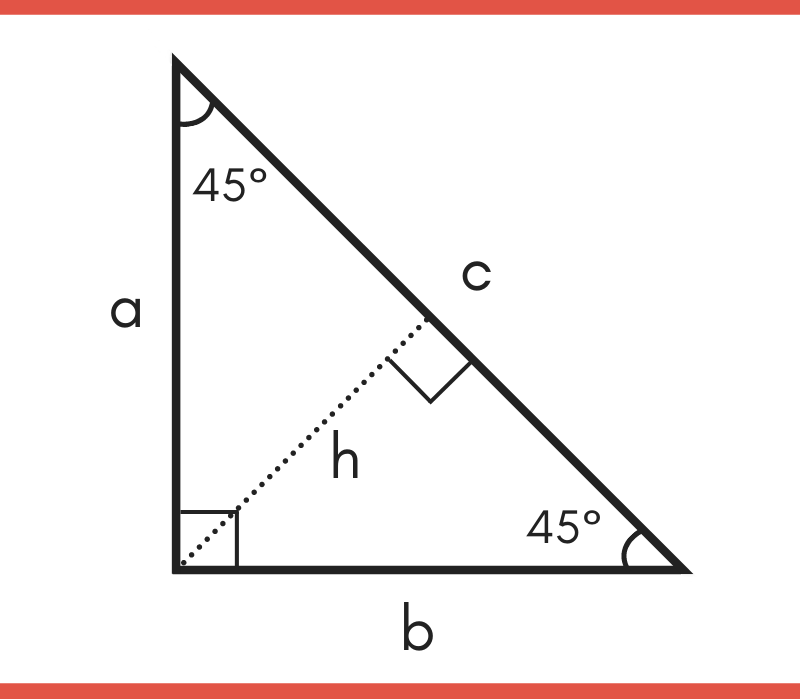



45 45 90 Special Right Triangle Calculator Inch Calculator




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Right Triangle Side Ratios Expii




Triangle Ruler Square Set 30 60 45 90 Degrees 22cm Triangle Rafter Angle Ruler 2 Pack Walmart Com




Pre Calculus Part 3 Trigonometric Function The Unit Circle And The 30 60 90 Degree Angles Youtube




A Triangle Has Three Angles 30 60 And 90 Degrees What Is The Value Of The Hypotenuse If The Long Leg Is 6 Feet Study Com



Right Triangles Gmat Free



1
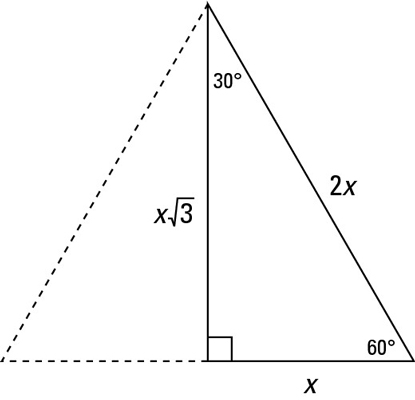



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Calculator Formula Rules




How To Construct A 30 60 90 Triangle With Compass And Straightedge Or Ruler Math Open Reference



Right Triangle Degrees 30 60 90 Clipart Etc
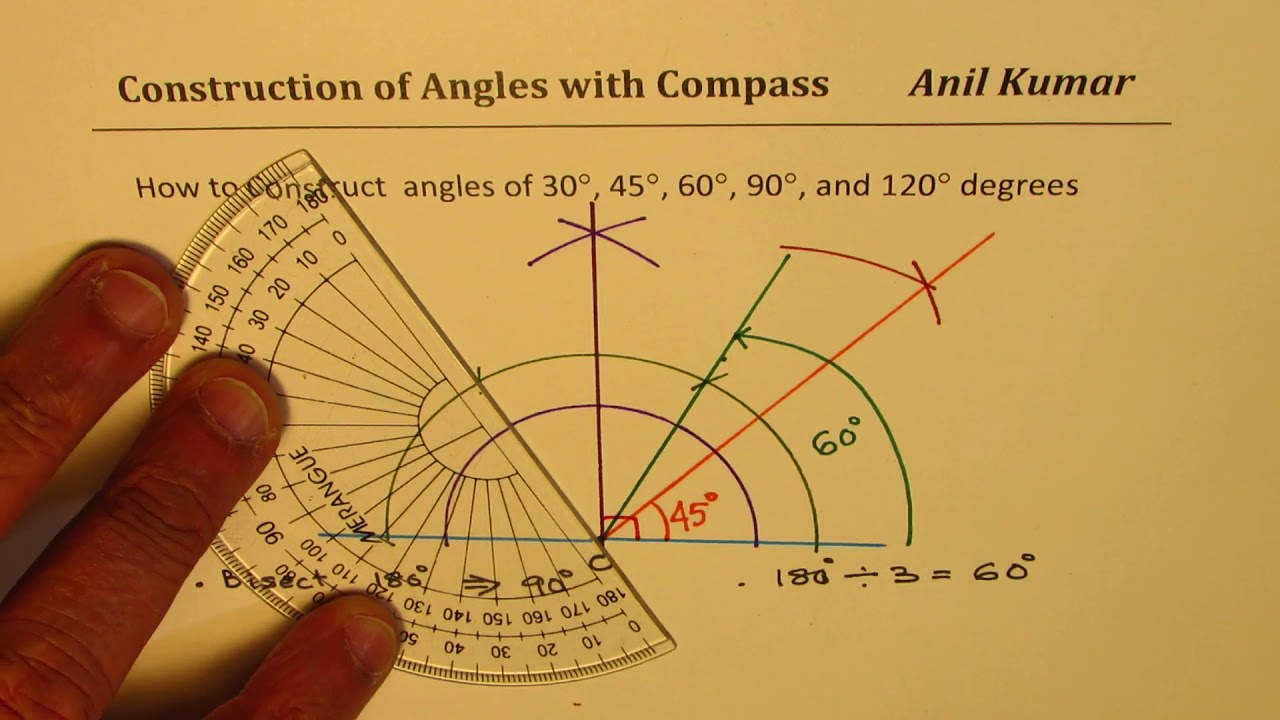



Construct Angles Of 30 45 60 90 1 Degrees With Compass Youtube



The Easy Guide To The 30 60 90 Triangle




The Complete Guide To The 30 60 90 Triangle



Why In A 30 60 90 Triangle Is The The Side Opposite 60 Degrees X Sqrt 3 Quora
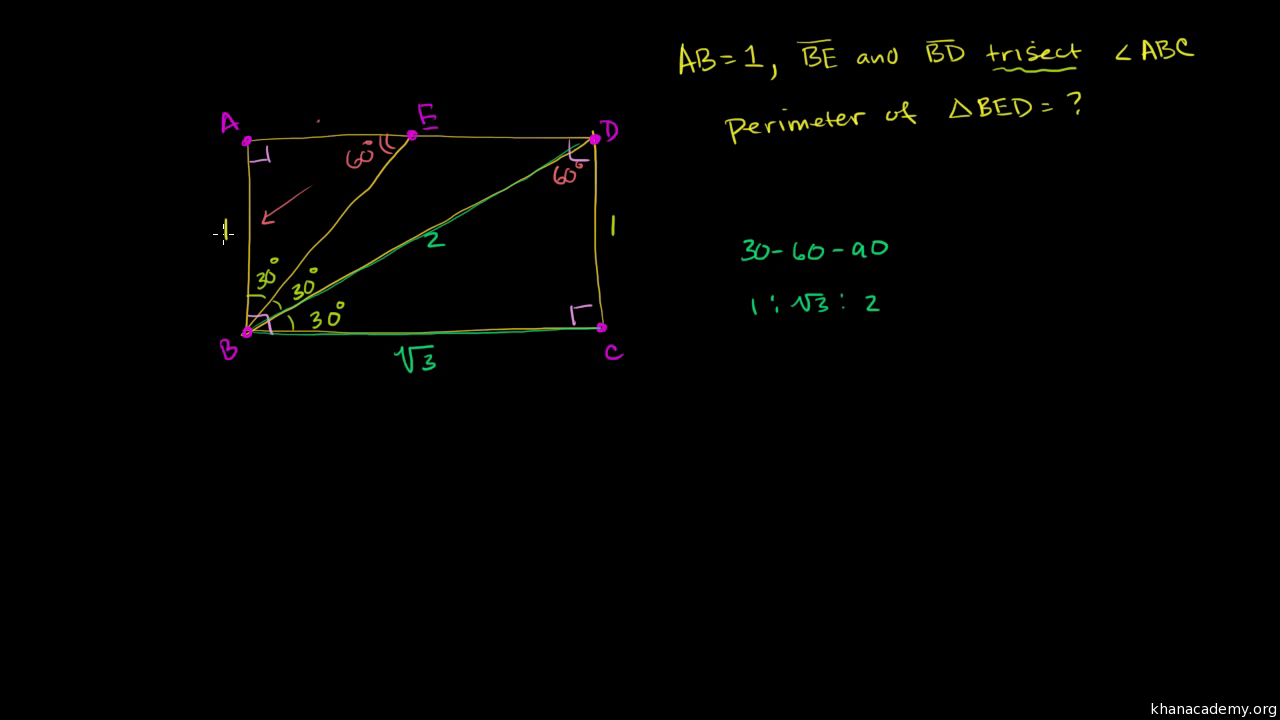



30 60 90 Triangle Example Problem Video Khan Academy
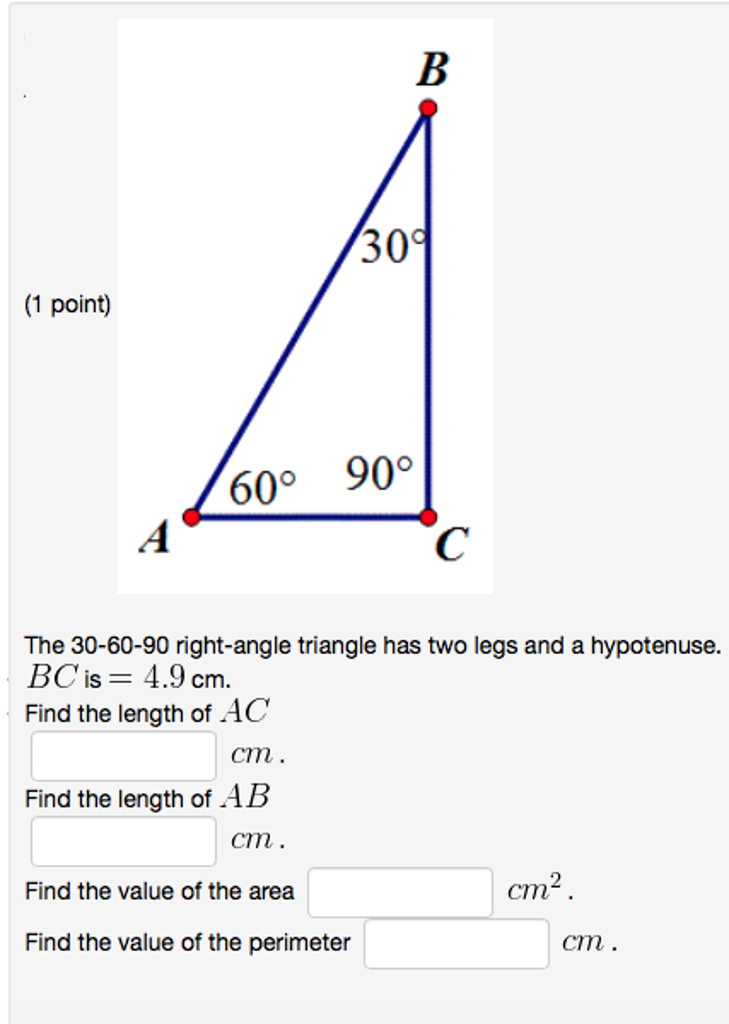



Solved 30 1 Point 60 90 The 30 60 90 Right Angle Chegg Com



The Easy Guide To The 30 60 90 Triangle




File 30 60 90 Triangle 2 Svg Wikimedia Commons
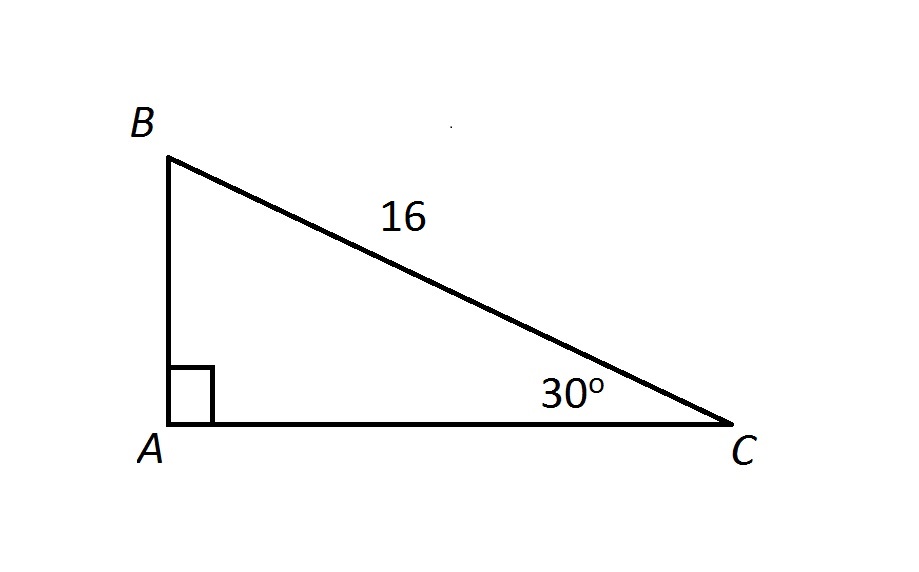



Special Triangles Hiset Math




Amazon Com Pacific Arc Drafting Triangle 4 Inch 30 60 90 Degrees Topaz Office Products



Geometry Problem 963 Right Triangle 30 60 90 Degrees Angle Bisectors Metric Relations Math Teacher Master Degree School College Sat Prep Elearning Online Math Tutor Lms




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Fully Explained W 19 Examples
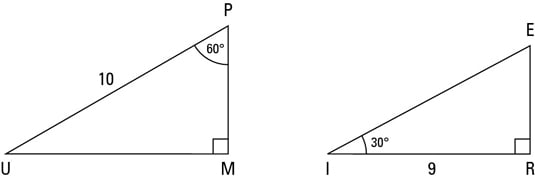



Identifying The 30 60 90 Degree Triangle Dummies
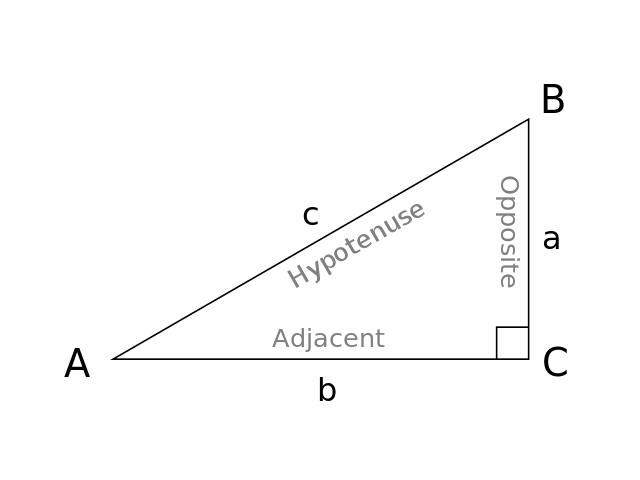



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Ratio Formula Video




Relationships Of Sides In 30 60 90 Right Triangles Read Geometry Ck 12 Foundation



1




A Quick Guide To The 30 60 90 Degree Triangle Dummies



30 60 90 Triangle Geometry



Solution In A Triangle Abc Angle A 30 Angle B 90 And Ab Is 12 Cm Find The Length Of




Triangles And Lines Special Right Triangles There Are Two Special Right Triangles 30 60 90 Degree Right Triangle 45 45 90 Degree Right Triangle Ppt Download



Math Figure 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
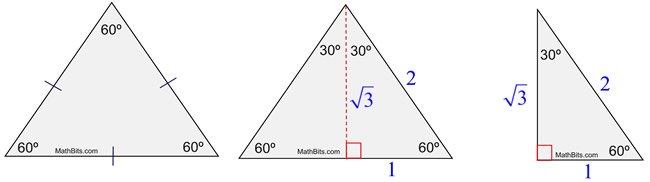



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Formulas Rules And Sides Science Trends



0 件のコメント:
コメントを投稿