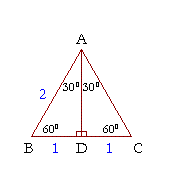
The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Visit https//wwwmathhelpcom/geometryhelpIn this video, we use the 45°45°90° and 30°60°90° triangle formulas to find the misAn equilateral triangle can be bisected into two 30° 60° 90° right triangles The height bisects the base and one angle of the triangle, creating two triangles that are congruent 30° 60° 90° right triangles Therefore, you only need the length of one side or the height to be able to find the area of an equilateral triangle

30 60 90 Triangles
Geometry 30 60 90 triangle formula
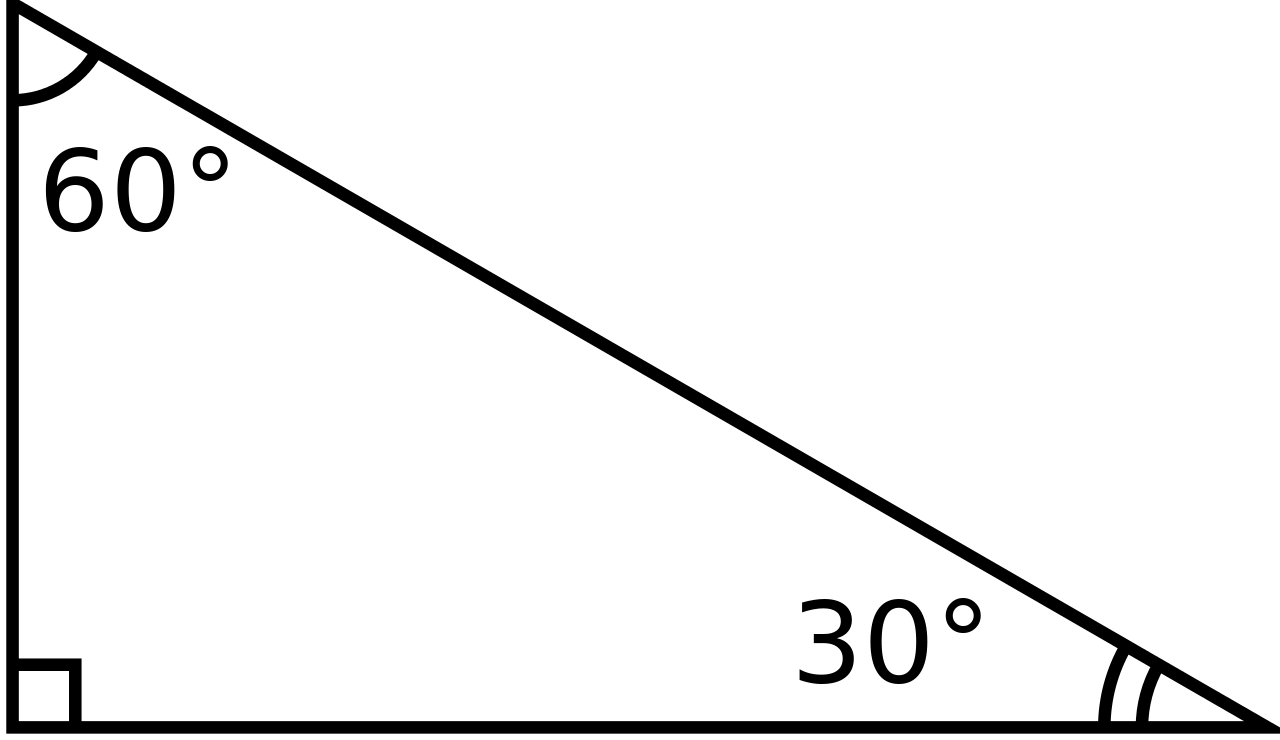
Geometry 30 60 90 triangle formula- 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2



1
A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three This special type of right triangle is similar to theSpecial Triangles The Triangle If you have one side, you can use these formulas (and maybe a little algebra) to get the others The Triangle If you have one side, you can use these formulas (and maybe a little algebra) to get the othersA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room
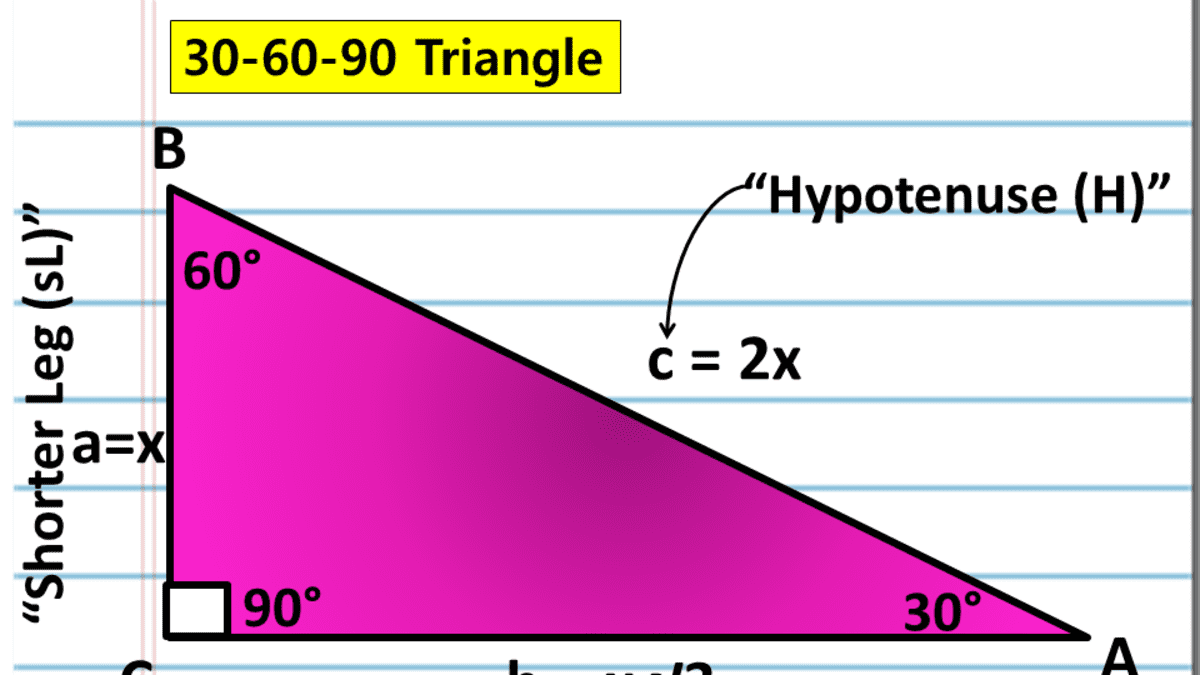
Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°) So while writing the ratio as 1 √3 2 would be more correct, many find the sequence 1 2 √3 easier to remember, especially when it is spoken See also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resizeIf you know that it's a triangle and the length of the side across from the smallest angle is 5, then you would be able to determine that the length of the other side is 5√3, or around 86 Then, you could plug these numbers into the equation to find that the area is ½ (5 x 86) = 215Distance formula dx=−()xy−()y 21 2 21 2 Slope of a line m yy xx = − − 21 21 Slopeintercept form of a linear equation ym=xb Pointslope form of a linear equation yy−=mx−x 11 Standard form of a linear equation AxBy=C STAAR GEOMETRY REFERENCE MATERIALS 30 ° 2 x x 60 ° x 3 30° – 60° – 90° triangle x x 45 ° 45
The basic triangle sides ratio is The side opposite the 30° angle x The side opposite the 60° angle x * √3 The side opposite the 90° angle 2x With this installment from Internet pedagogical superstar Salman Khan's series of free math tutorials, you'll learn how to work with 30°60°90° right triangles Video Loading Video Loading (1) Part 1 of 2 How to Work with 30°60°90° triangles in geometry, (2) Part 2 of 2 How to Work with 30°60°90° triangles in geometryDistance formula Slope of a line Slopeintercept form of a linear equation Pointslope form of a linear equation Standard form of a linear equation STAAR GEOMETRY REFERENCE MATERIALS 30 ° 2 x x 60 ° x 3 x x 45 ° 45 ° x 2 A C B COORDINATE GEOMETRY RIGHT TRIANGLES d x x y y= − −( ) ( ) 2 1 2 2 1 2 y y mx x− = − 1 1 ( )



30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°) Click to A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherUsing what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected item



File 30 60 90 Triangle 2 Svg Wikimedia Commons




Special Right Triangles Review Article Khan Academy
Right Triangles 30 60 90 Special Right Triangles Notes and Practice This packet includes information on teaching 30 60 90 Special Right Triangles I have included *** Teacher Notes with worked out formulas, diagrams and workout examples(the diagram onA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and the longer leg is the square root of 3 timesAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles




Tenth Grade Lesson 30 60 90 Triangles Betterlesson



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Area of a Triangle The formula to calculate the area of a triangle is = (1/2) × base × height In a rightangled triangle, the height is the perpendicular of the triangle Thus, the formula to calculate the area of a rightangle triangle is = (1/2) × base × perpendicularA right triangle is a special case of a triangle where 1 angle is equal to 90 degrees In the case of a right triangle a 2 b 2 = c 2 This formula is known as the Pythagorean Theorem In our calculations for a right triangle we only consider 2 known sides to calculate the other 7 unknowns In this triangle, the shortest leg ($x$) is $√3$, so for the longer leg, $x√3 = √3 * √3 = √9 = 3$ And the hypotenuse is 2 times the shortest leg, or $2√3$) And so on Đang xem Geometry triangle practice The side opposite the 30° angle is always the smallest, because 30 degrees is the smallest angle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
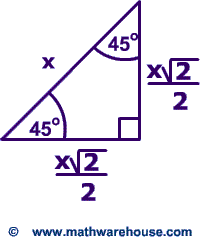
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that belowThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2
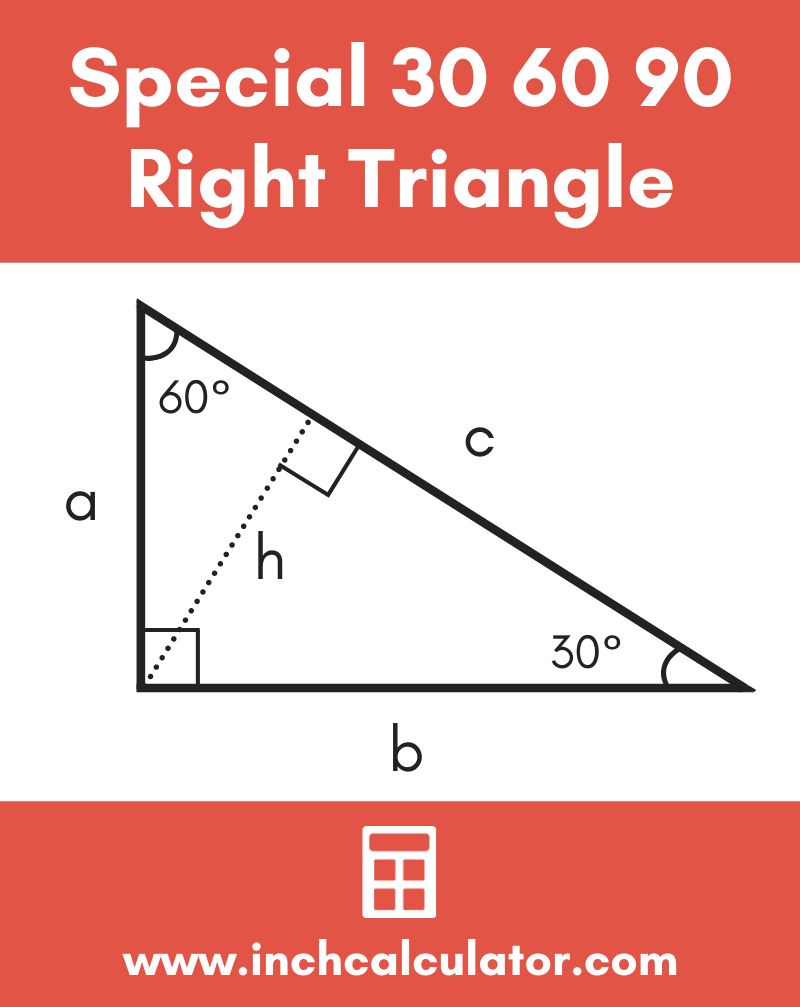



30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Calculator Formula Rules
Example We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse $$7\cdot \sqrt{2}\approx 99$$ In a 30°60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formula Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 x Geometry Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60°




30 60 90 Triangle Theorem Ratio Formula Video
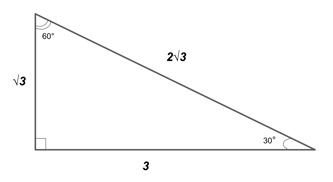



The Easy Guide To The 30 60 90 Triangle
The area of a triangle formula is 1/2 × b × h Substituting b = 12 units and h = 5 units, we have, Area =1/2 × 12 × 5 = 30 units 2 Therefore, the area of the right triangle is 30 square unitsStart studying formulas for Geometry SOL Learn vocabulary, terms, and more with flashcards, games, and other study tools Home rules for triangle leg=x hypotenuse=x√2 rules for triangle short leg=x long leg=x√3 hypotenuse=2x angleA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle
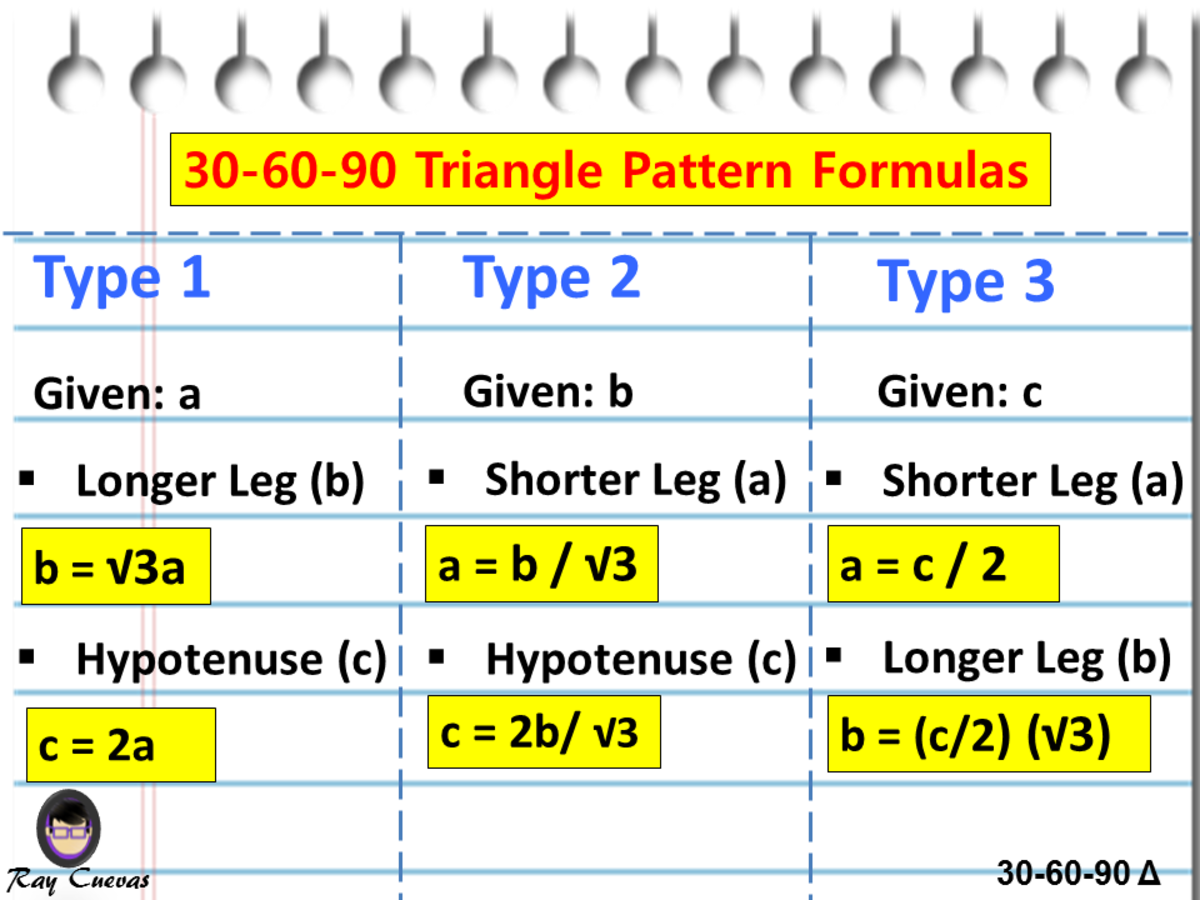



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
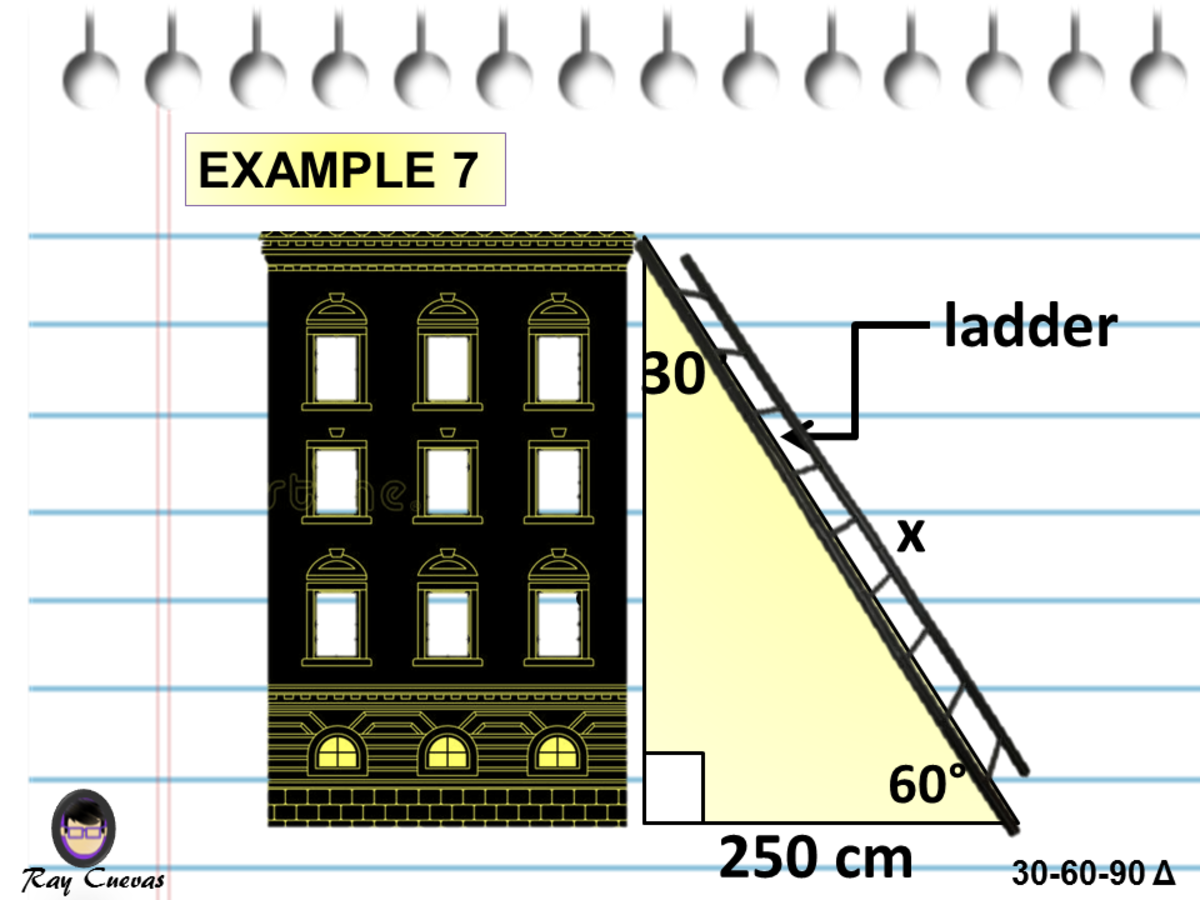



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
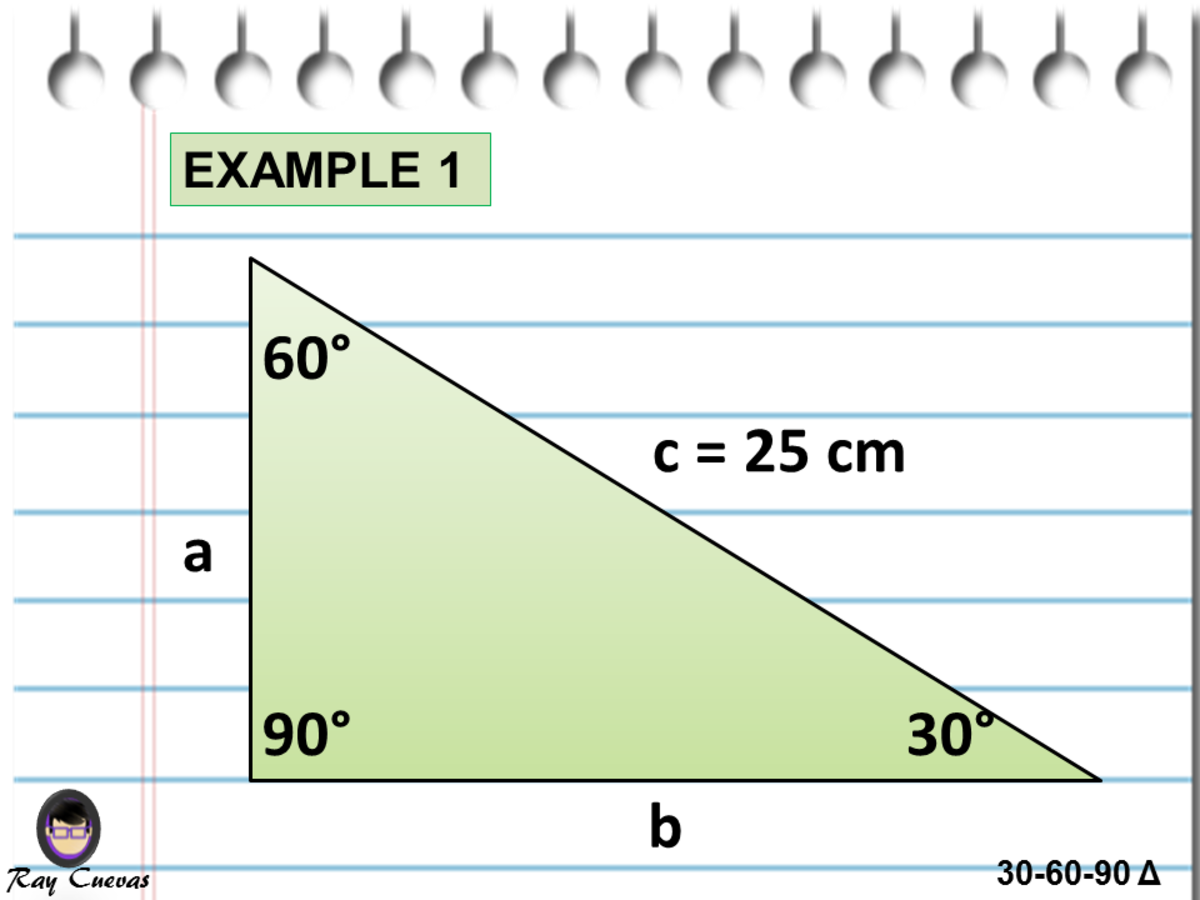
The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use60° 60° 30° 30° tt 2t h 2t FIGURE 7 3 If the hypotenuse of a 30 ° – 60 – 90 triangle is 12, fi nd the other 2 sides Answer 3 6, 6 √ — 3 5 10 60° 30° 5√‾3 FIGURE 8 Defi nition A radical expression is in simplifi ed form if 1 There are no perfect squares that areWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI




Right Triangles 30 60 90 Special Right Triangles Notes And Practice




30 60 90 Triangle Formulas Rules And Sides Science Trends
Mrs Lin These are the two most common right triangles For degrees, the ratio is 1 1 √ 2 For degrees, the ratio is 1 √ 3 2 Other concepts to remember are that in any triangle a larger angle corresponds to longer side and bsame angles have the same side lengthThe reason these triangles are considered special is because of the ratios of their sides they are always the same!The 30 – 60 – 90 degree triangle is in the shape of half an equilateral triangle, cut straight down the middle along its altitude It has angles of 30°, 60°, and 90° and sides in the ratio of The following figure shows an example Get acquainted with this triangle by doing a couple of problems




30 60 90 Triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies
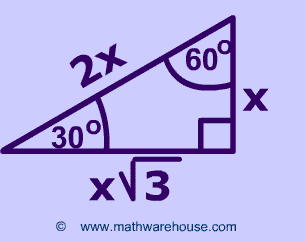
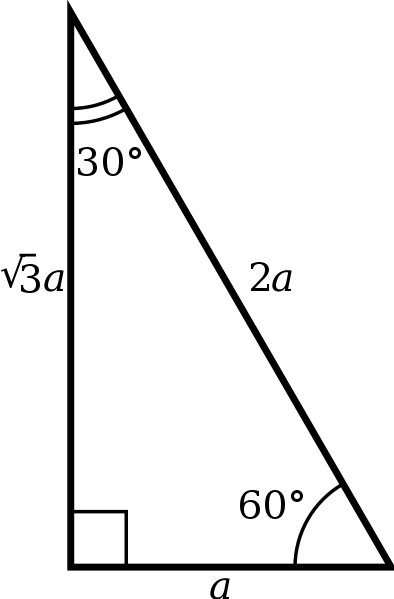
Triangle $x, x√3, 2x$ Just like with an isosceles right triangle, a triangle has side lengths that are dictated by a set of rulesWhat is the 30 60 90 triangle formula?Formula for finding the hypotenuse triangle Formula for finding the hypotenuse triangle 2(shorter leg) I pair of parallel lines Trapezoid 2 pairs of parallel lines Bundle Elementary Geometry for College Students, 5th Math Study Skills Workbook, 4th




Right Triangles 30 60 90 Special Right Triangles Notes And Practice




Geometry 8 4 Special Right Triangles This Is
About This Quiz & Worksheet Triangles that have 30, 60, and 90 degree angles have specific and unique characteristics This interactive quiz will use multiple choice questions, including practice Right triangles are one particular group of triangles and one specific kind of right triangle is a right triangle As the name suggests, the three angles in the triangle are 30, 60Special triangles – Formula and examples Special triangles are right triangles that have special proportions for their sides The 30°60°90° triangle has the proportions 1√32 The 45°45°90° triangle has the proportions 11√2 All the lengths of these sides can be easily found if we only know the length of one of the sides




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Explanation Examples
Special right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangleSpecial right triangles 30 60 90 math30 60 90 theorems about special right triangles 45 45 90 and 30 60 90 degree triangles this video discusses two special right triangles how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side and then does a few examples using them The hypotenuse is equal to twice the length of the shorter leg, which is the side across from the 30 degree angle The longer leg, which is across from the 60 degree angle, is equal to multiplying the shorter leg by the square root of 3 This picture shows this relationship with x representing the shorter leg




Kutasoftware Geometry Special Right Triangles Part 2 Youtube



1
Need more Geometry help?Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
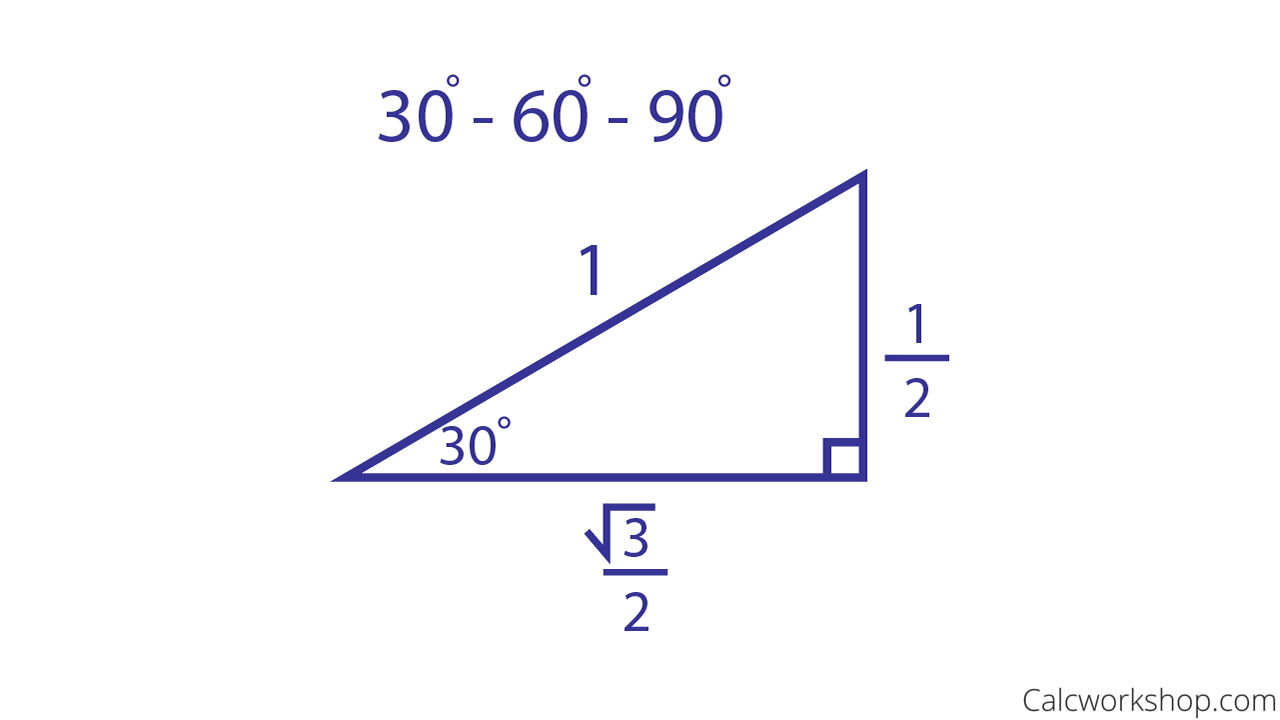



Unit Circle W Everything Charts Worksheets 35 Examples



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



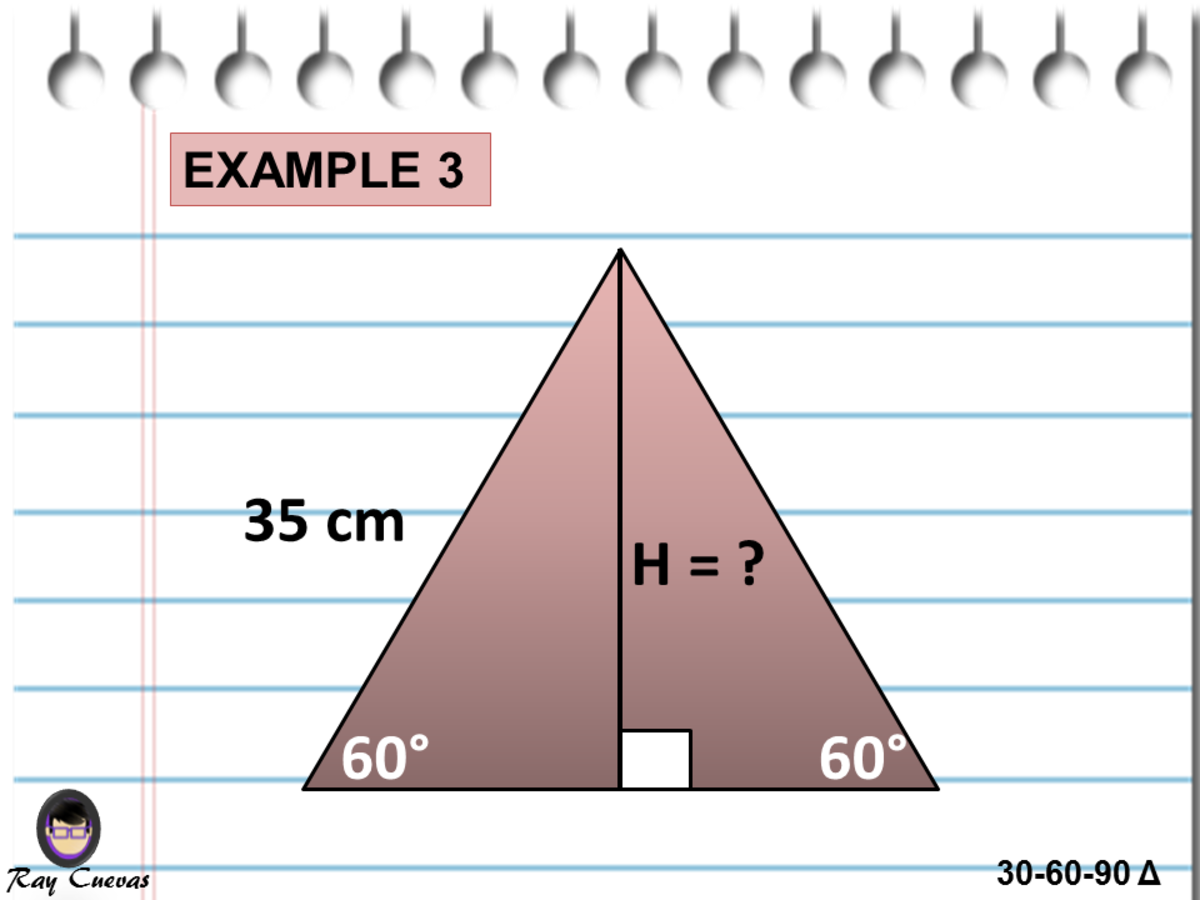
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
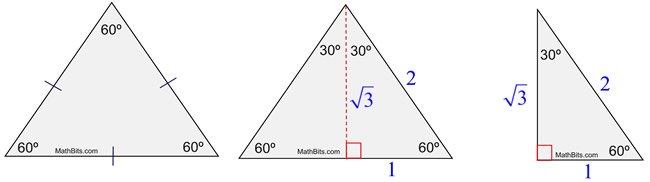



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Geometry Help From Mathhelp Com 30 60 90 Triangles Youtube
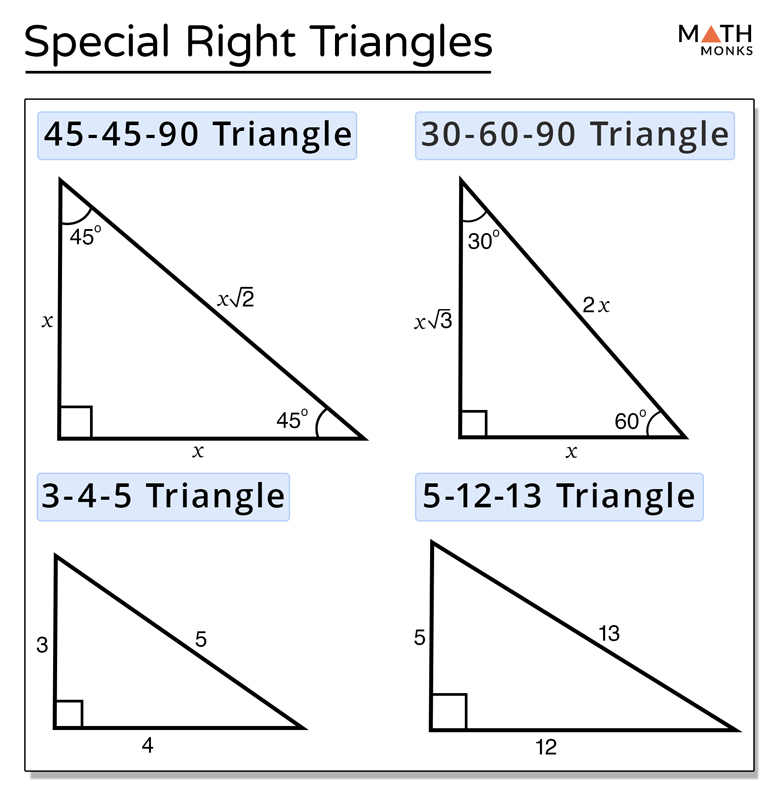



Special Right Triangles Definition Formula Examples




30 60 90 Triangle Calculator Formula Rules
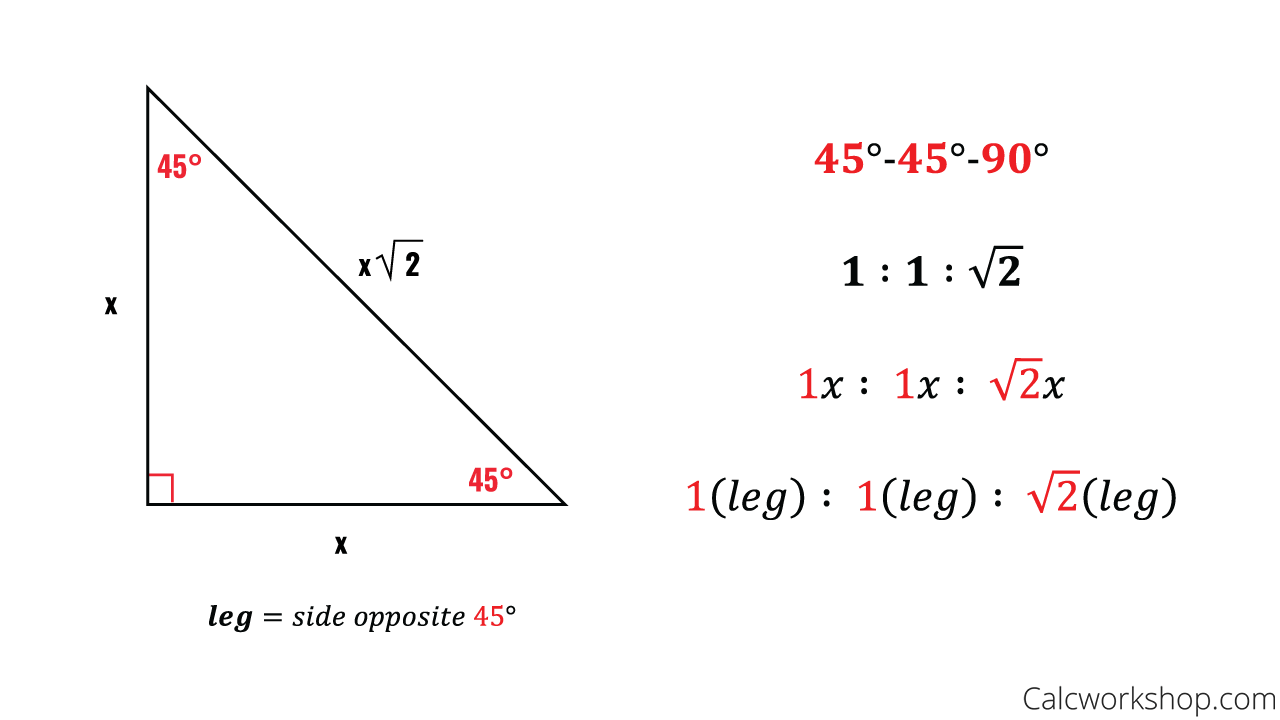



Special Right Triangles Fully Explained W 19 Examples
.JPG)



Ms Liefland Harper Junior High Geometry 12 3 Through 12 7



1




Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
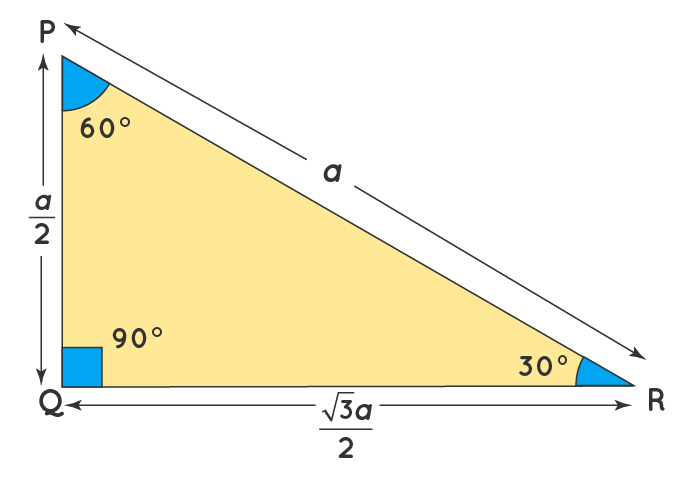



30 60 90 Triangle Definition Theorem Formula Examples



1




30 60 90 Triangle Calculator Formula Rules




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math
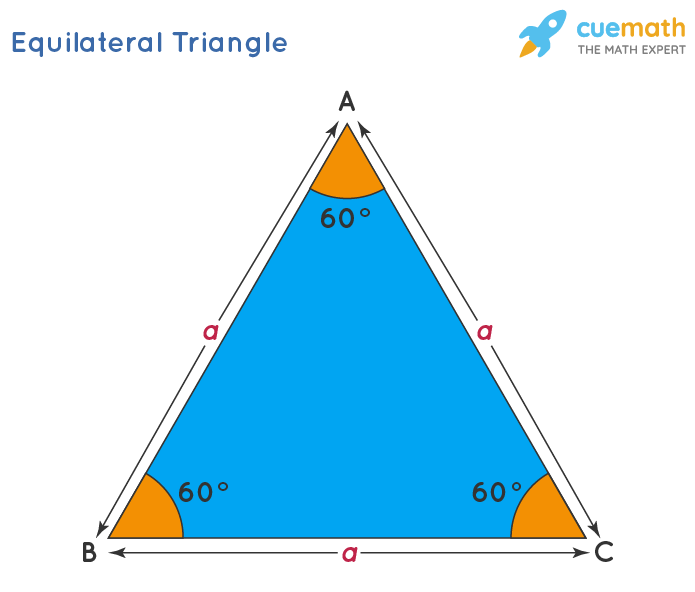



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Explanation Examples
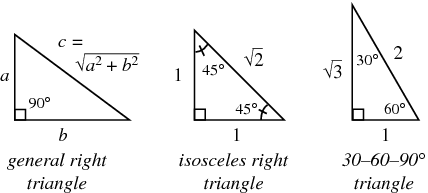



Right Triangle From Wolfram Mathworld




Special Right Triangles Use As An Extension To Conventional Pythagorean Theirem Right Triangle Gre Math Geometry Lessons



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Right Triangles Gmat Free



30 60 90 Triangle Formulas Rules And Sides Science Trends



Special Right Triangles Intro Part 2 Video Khan Academy



30 60 90 And 45 45 90 Triangle Calculator
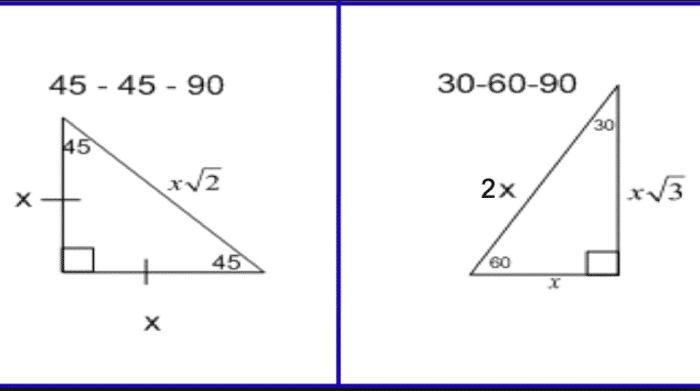



Special Right Triangles Complete Reference Guide The Education




The Complete Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangle Wikipedia




30 60 90 Triangle Theorem Ratio Formula Video




Learn About The 30 60 90 Triangle Caddell Prep Online




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Calculator Formula Rules
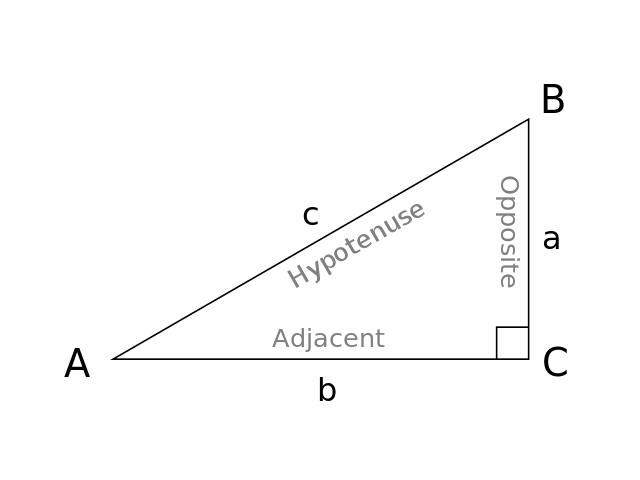



30 60 90 Triangle Formulas Rules And Sides Science Trends




Special Right Triangles Review Article Khan Academy




Special Right Triangles Proof Part 1 Video Khan Academy




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Theorem Ratio Formula Video



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Definition Theorem Formula Examples




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Ratio Formula Video



1




30 60 90 Triangle Theorem Ratio Formula Video
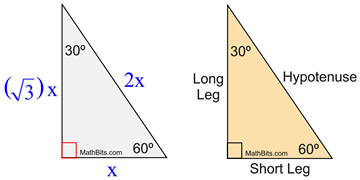



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Definition Theorem Formula Examples



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




How To Find The Area Of A Right Triangle Basic Geometry




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Right Triangles Free Math Help




How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor




30 60 90 Special Right Triangle Calculator Inch Calculator



30 60 90 And 45 45 90 Triangle Calculator



Special Right Triangle 30 60 45 45 37 53 Elearning




The Complete Guide To The 30 60 90 Triangle
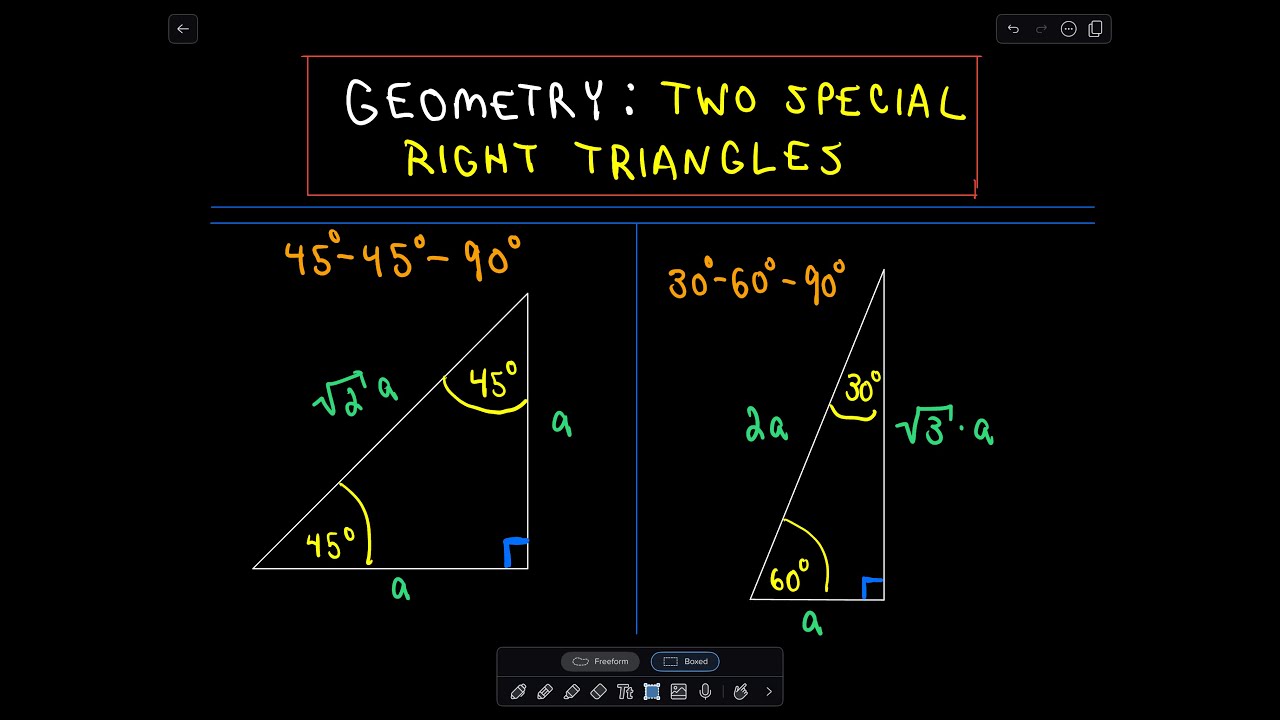



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




5 30 60 90 Triangles Geometry15a



How To Work With 30 60 90 Degree Triangles Education Is Around
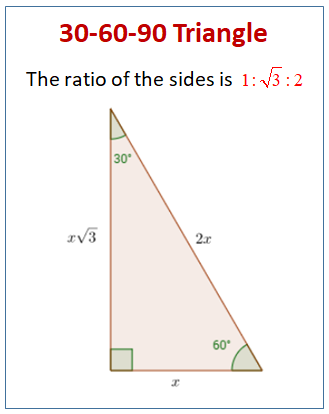



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




Special Right Triangles Video Lessons Examples And Solutions




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
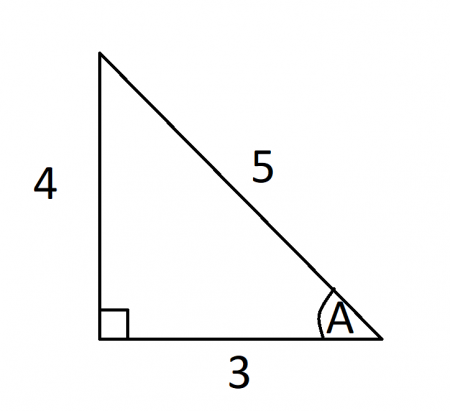



30 60 90 Triangle Formulas Rules And Sides Science Trends
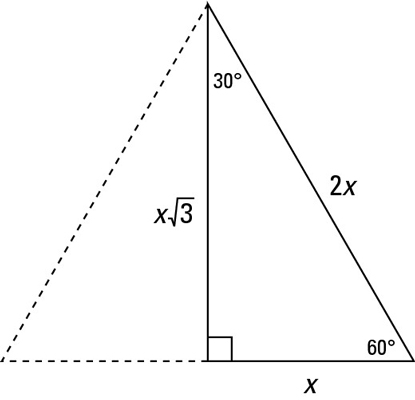



Identifying The 30 60 90 Degree Triangle Dummies
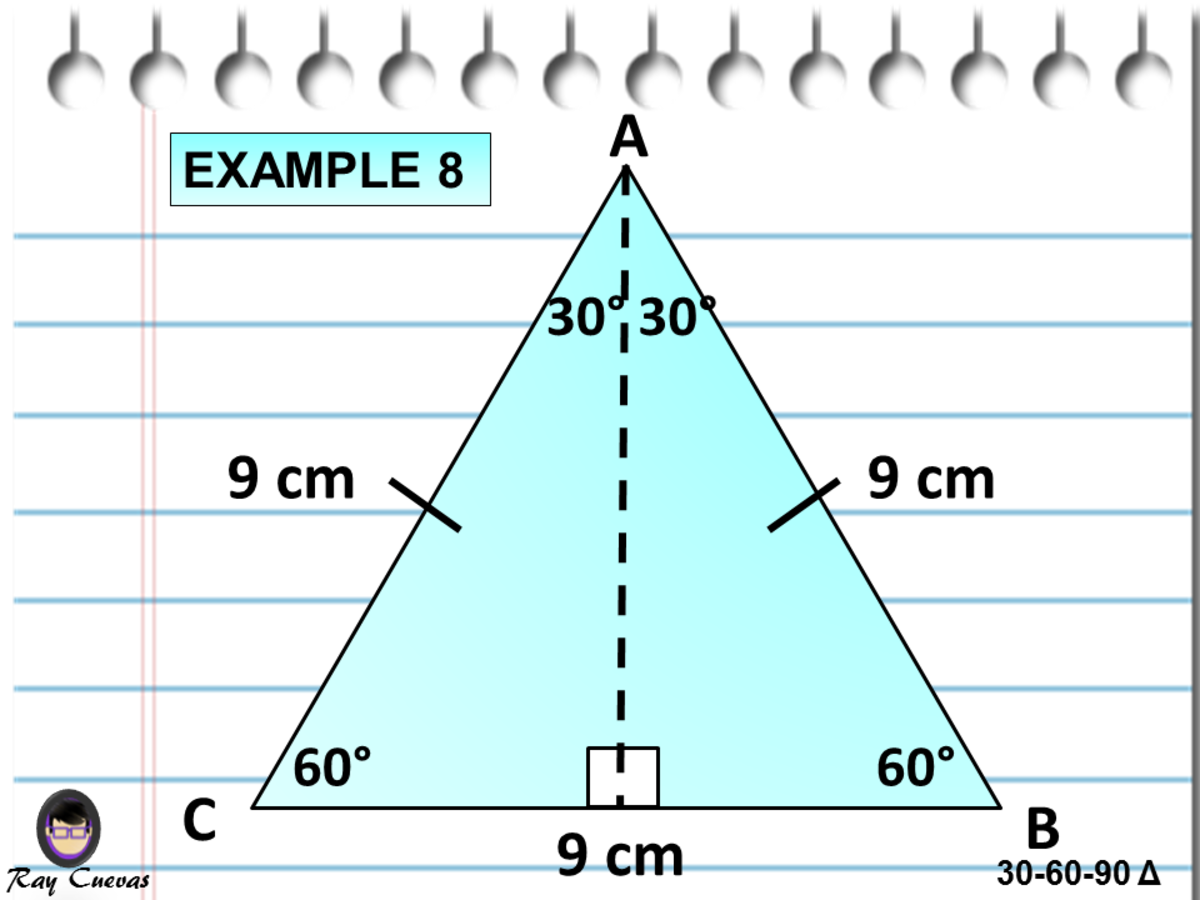



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle



Solve A 30 60 90 Triangle With Gradea




30 60 90 Right Triangle Side Ratios Expii



0 件のコメント:
コメントを投稿